NMR Spectroscopy Primer
This page describes some of the terms and concepts commonly used in NMR spectroscopy (particularly multinuclear NMR), many of which are referred to in other pages.
Quick Jump: Coupling patterns | Mutual Coupling | Satellites | Decoupling | Berry pseudorotation
Coupling patterns, singlet, doublet, triplet ... multiplets and Pascal's triangle
When coupling occurs between different magnetically-active nuclei (I > 0) then characteristic patterns arise. Generally if a nucleus couples with n spin-active nuclei each with a spin-quantum number, I, then (2nI+1) lines will be seen. This equation can be simplified, and often is in organic chemistry applications, if I = 1/2 to (n+1) lines - however we prefer to use the full form of the equation, since that applied in all cases. The relative intensities of the set of lines when I = 1/2 is given by Pascal's triangle (see below). So coupling to 1 spin-1/2 nucleus, such as a proton, or fluorine nucleus would result in the appearance of a doublet (two peaks in the ratio 1:1), coupling to two spin-1/2 nuclei gives a 1:2:1 triplet, while coupling to three equivalent I=1/2 nuclei would give a quartet (four peaks in the ratio 1:3:3:1). You can generate more patterns like this using the j-splitting calculator below.
If I > 1/2 (called "quadrupolar nuclei") then the same 2nI+1 'rule' applies; that is coupling to, for example 3 I=1 nuclei will give a 7-lined pattern. How do you calculate the nmr splitting pattern for qaudrupolar nuclei? The relative intensities of the lines are obtained by extending Pascal's triangle to allow for each nucleus having more than two possible spin-states. There are a number of ways of doing this, including a method called the "sliding window" method, which is used in our pattern generator below:
You can see the effects of coupling using our NMR coupling pattern generator (2nI+1 calculator) below:
2nI+1 = 2*6*0.5+1 = 7 lines.1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
The names of the patterns generated depends on the total number of lines, as listed below:
1 line : singlet2 lines: doublet
3 lines: triplet
4 lines: quartet
5 lines: quintet (sometimes pentet)
6 lines: sextet
7 lines: septet (sometimes heptet)
8 lines: octet etc...
Mutual Coupling - the 19F and 31P NMR spectra of K[PF6].
When you observe the spectrum of one spin-active nucleus which is coupled to one, or more, other spin-active nuclei then the patterns described above occur. This coupling is the same which ever nucleus you observe, so the size of the coupling constant (measured in Hz) is the same which ever spectrum you record. This is because the coupling is mutual - the same for both.
As an example, the spectra below were recorded for a solution of K[PF6] in DMSO. The six fluorines are all equivalent in the [PF6]- anion and so the 31P NMR spectrum consists of a septet. The separation between any adjacent pair of peaks is the P-F coupling constant, in this case 711 Hz. Since all six fluorine nuclei are equivalent they couple to just the phosphorus nucleus to give a doublet, again separated by 711 Hz.
Thus the two nuclei are said to exhibit mutual coupling, that is they couple to each other in the same way. The PF coupling constant labelled as 1J(PF) [where the superscript 1 refers to the 1 bond between the P and F nuclei] is 711 Hz. [Note: coupling constants are always quoted in Hz (which is independent of the spectrometer frequency) not ppm! While the chemical shift is reported in ppm as the position of the centre of the pattern.]
Satellites
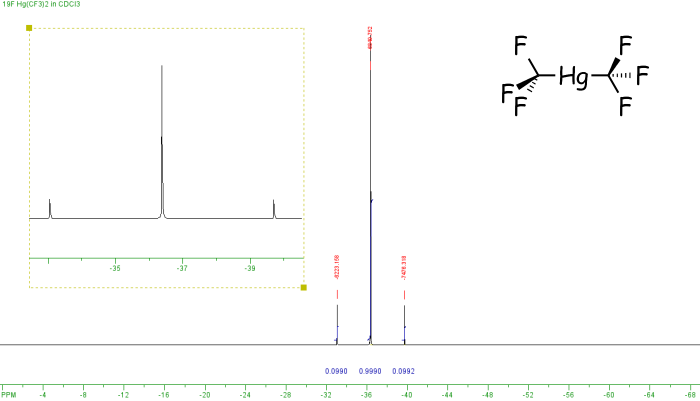
In the example above both fluorine and phosphorus are 100% spin-active, however this is not the case for all elements. If a non-100% abundant nucleus is spin-active then satellites are observed. these are smaller peaks that appear either side of the main peak. For example, the spectrum below is of Hg(CF3)2. It shows three peaks which arise as follows. Mercury has a number of different isotopes, one of these 199Hg is spin-active (I=1/2) but only 16.8% abundant. So of all the molecules of Hg(CF3)2, 83.2% (100% - 16.8%) will not contain spin-active mercury, and so the six equivalent fluorine nuclei will not couple to any other spin-active nuclei, so a singlet is observed. However, for the 16.8% of molecules containing 199Hg coupling will occur between the 199Hg and 19F nuclei, so a doublet would arise (2nI+1 = 2). The actual spectrum observed is a combination of these two components - a singlet [83.2%] and a doublet [total intensity 16.8%, ie 8.4% each line] with a similar chemical shift value, so one peak of the doublet appears either side of the singlet.
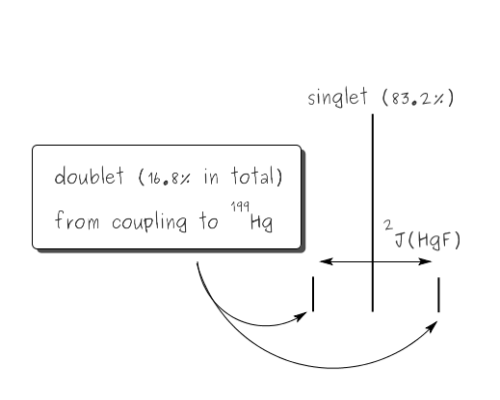
The derivation of mercury satellites
The 2J(HgF) coupling constant is measured across the doublet, ie from one satellite peak to the other, in this case that is 1253 Hz. We can also check the relative intensities, since the signals due to 199Hg are the outer, weaker peaks, and these add up to 0.0990 + 0.0990. However the intensities of all three peaks corresponds to all of the molecules. So the proportion of spin-active mercury is equal to the sum of the intensities of the satellite peaks divided by the total intensity, ie (0.0990 + 0.0992) / (0.0990 + 0.999 + 0.0992) = 16.5%.
Decoupling
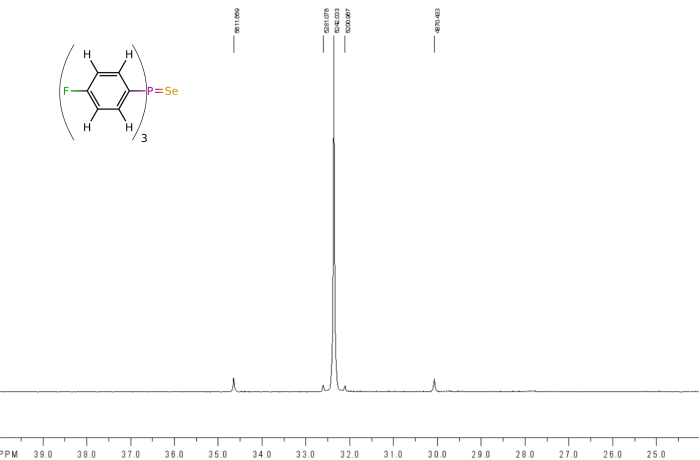
It is often useful to remove some of the couplings that might be present in an NMR spectrum to simplify the observed spectra. This is done at the time the data is recorded, and usually is limited to removing coupling to proton nuclei, so is called proton-decoupling. It is denoted by putting the decoupled nucleus in curly brackets, eg 13C{1H}, which means that the carbon NMR spectrum will show no coupling to any of the protons. It is also common to record phosphorus NMR spectra with proton decoupling, ie 31P{1H}, and an example of the difference that this can make is shown below for the phosphorus NMR spectra recorded of (4F-C6H4)3PSe, shown on the spectra.
The second spectrum is of the same cimpound, but now recorded as a proton-decoupled spectrum. Because this removes all the coupling between the phosphorus and proton nuclei, the spectrum simplifies to the point where now the selenium satelites are obvious and even the smaller 13C NMR satelites are now visible.
Berry pseudorotation
Compared with a number of other spectroscopic techniques NMR spectroscopy is relatively slow, so there is a chance that a molecule may be rearranging more quickly than the rate at which the spectroscopic process is occuring. If this happens then data for a time-averaged structure will be recorded.
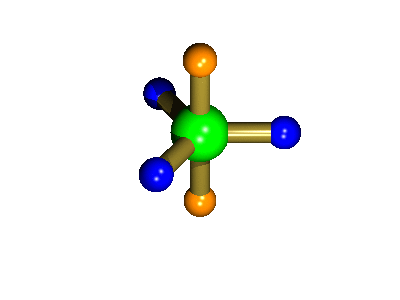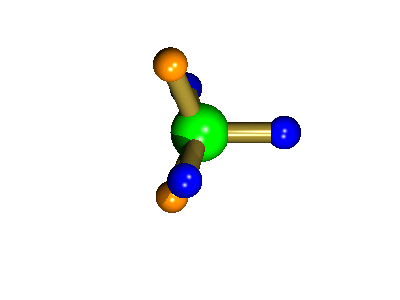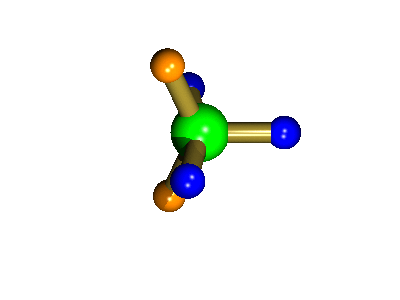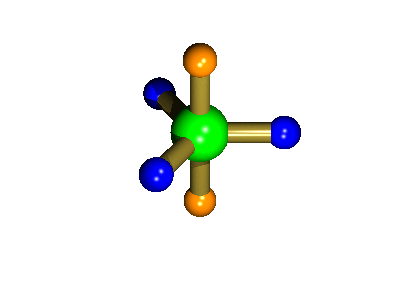
Probably the most widely cited, inorganic, examples of such behaviour are the 5-coordinate molecules that adopt a trigonal bipyramidal structure, such as PF5. As shown below (left), these have (in a static structure) two environments, the two axial fluorines (orange) and three equatorial fluorines (blue). However, the 31P NMR spectrum of this molecule, recorded at room temperature, shows a sextet, suggesting that all 5 fluorines are equivalent. This occurs, because the molecule is in motion, via a square-based pyramidal intermediate (picture 2) that gives rise to an averaging, such that the axial and equatorial environments swap over (see picture 3).
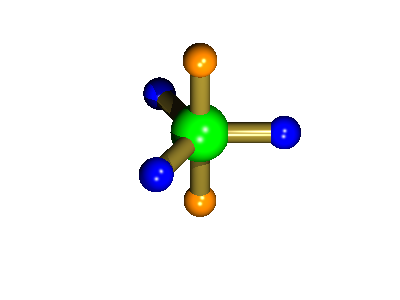
Starting point, axial fluorine substituents are orange
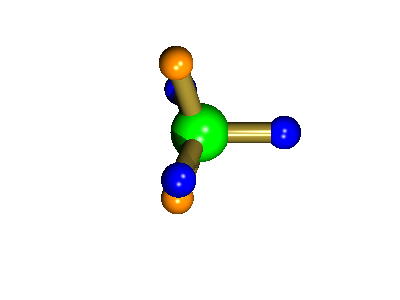
The square-based pyramid intermediate
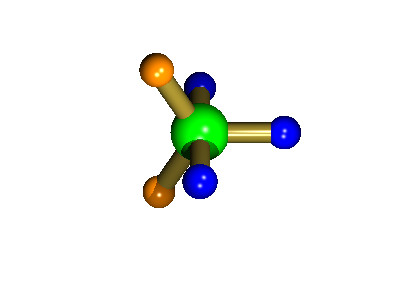
Orange substituents are now equatorial
The whole of this process is illustrated below based on a POVRay generated movie. During the motion the two axial (orange) fluorines become equatorial, along with one of the blue atoms, while the other two blue coloured fluorines end up as the two axial substituents. In this way the positions of the fluorine atoms constantly change between being axial and equatorial, ie they become chemically equivalent.

![31P NMR spectrum of K[PF6] 31P NMR spectrum of KPF6, click to expand](/pics/31P_NMR_PF6.png)
![19F NMR spectrum of K[PF6] 19F NMR spectrum of KPF6, click to expand](/pics/19F_NMR_PF6.png)

![Fluorous dominated structure of [AuCl{Et2P(CF=CF2)}] The crystal packing diagram of [AuCl{Et2P(CF=CF2)}]](/rotator/aurophilicity.png)
